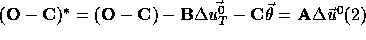
Rappelons que la répartition des observations Hipparcos n´est pas homogène mais que celles-ci sont regroupées en fonction du référentiel intermédiaire utilisé, c´est à dire d´un RGC donné. Considérons le système réduit suivant:
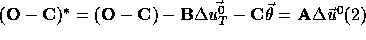
où 
et
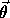sont ici les solutions obtenues par moindres carrés classiques.
On forme ainsi les quantités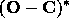 
, que l´on appelera O-C
``réduits" du système.
La répartition non homogène des O-C est la cause du mauvais conditionnement du système. Celui-ci peut être mis en évidence de la manière suivante:
La matrice de correlation a priori.
A partir du système (2), on peut former la matrice de corrélation a priori relative à la petite planète considérée. Celle-ci permet de mettre en évidence la présence de corrélations élevées entre certaines inconnues du système: ainsi, des corrélations supérieures à 0.90 sont fréquentes. A titre d´exemple, la matrice de corrélation a priori de la petite planète 349-Dembowska est donnée dans la table 2.
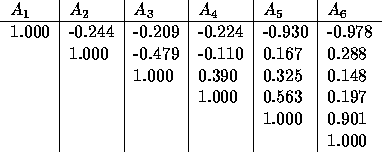
Table: Matrice de corrélation pour la petite planète Dembowska.
Valeurs propres et nombres de condition.
La connaissance des valeurs propres de la matrice
de corrélation (soit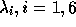 
) entraîne celle
des nombres de condition donnés par:
Un nombre de condition supérieur à 30 trahit un système mal conditionné. Dans le cas de la petite planète Dembowska par exemple, les nombres de condition ont pour valeur 121; 11.2; 2.88; 2.04; 1.38 . De manière plus générale, la quasi totalité des petites planètes observées par Hipparcos ont une matrice de corrélation possèdant au moins une valeur propre nulle. Or la résolution du système réduit (2) passe par l´inversion de cette matrice... On comprend dès lors que cette résolution soit difficile.
Notons cependant que notre étude ne porte que sur des données partielles et qu´à l´issue de la mission Hipparcos certaines inconnues seront décorrélées. Pas toutes, loin s´en faut.
Décomposition en valeurs singulières
L'étude des matrices de corrélation permet la connaissance de leur rang (en général différent de 6). On peut alors projeter le système (1) sur une nouvelle base prenant en compte les rangs de ces différentes matrices. Ce faisant, seules les inconnues relatives aux éléments de la Terre et à la rotation du repère Hipparcos sont conservées, les corrections aux éléments orbitaux des petites planètes étant remplacées par des combinaisons linéaires du type:
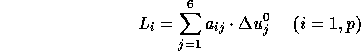
où p est le rang de la matrice de corrélation de la planète
et les 
sont les composantes de ses vecteurs propres.
On pourra se reporter à
Bec Borsenberger
et al., (1994) pour un
exposé précis de la
méthode et les résultats obtenus . Notons l´avantage d´une telle approche dans
les problèmes à grand nombre d´inconnues lorsque celles-ci ne
présentent pas toutes le même intérêt.
On peut ainsi améliorer la détermination d´un
certain nombre d´entre elles au détriment des autres.