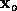 la solution des moindres carrés et
la solution des moindres carrés et 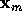 la solution de dimension moindre, et soit les équations de conditions écrites sous la forme matricielle :
la solution de dimension moindre, et soit les équations de conditions écrites sous la forme matricielle :

L´intervalle de temps sur lequel se répartissent les observations des
astéroïdes est relativement restreint comparé à leur période de
révolution,
de plus le cercle de balayage oscille autour d´un plan perpendiculaire à
l´écliptique. Il s´en suit que seuls les paramètres associés à l´orientation
de la trajectoire des petites planètes sont très bien déterminés, les
inconnues
relatives aux corrections des autres paramètres (demi-grand axe, excentricité,
anomalie moyenne et argument du périhélie) sont par contre fortement
corrélés. Puisque les planètes sont observées au voisinages des quadratures,
elles présentent une phase ce qui introduit un biais entre les positions
calculées et les positions déduites des observations (Morando and Lindegren, 1989). La modélisation du
déplacement du photocentre (écart sur le ciel entre le centre de gravité et
le photocentre) se fait en considérant la planète sphérique et de surface
homogène. Pour chaque planète on décompose la forme quadratique associée à
la matrice normale sur ses axes
principaux ; les inconnues du problème sont, par ces changements de variables, des
combinaisons linéaires des variations sur les éléments osculateurs. Ceci peut se faire sans le calcul
explicite de la matrice normale, à partir de la décomposition en valeurs
singulières de la matrice des équations de conditions.
Les fortes corrélations
font que pour la plupart des planètes les corrections sur les ne sont pas
déterminées de manière unique. On ne cherche pas à calculer les variations des
six mais le nombre minimal de paramètres pouvant modéliser les écarts entre
les positions observées et les positions calculées. Pour chaque planète on
supprime successivement les paramètres associés aux petites valeurs singulières ;
on obtient ainsi à chaque étape les résidus correspondants à une solution de dimension moindre. On détermine enfin le nombre minimal de paramètres en
appliquant le test de Fisher (rapport de variances) sur les différents résidus
obtenus. Soit 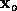 la solution des moindres carrés et
la solution des moindres carrés et 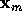 la solution de dimension moindre, et soit les équations de conditions écrites sous la forme matricielle :
la solution de dimension moindre, et soit les équations de conditions écrites sous la forme matricielle :

on a les deux propriétés :
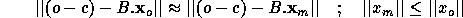
La solution 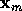 est donc la solution de norme minimale qui "minimise" la norme des résidus.
est donc la solution de norme minimale qui "minimise" la norme des résidus.
