



Next: Representation of the
Up:
A Theory of
Previous:
A Theory of
The Saturn's seventh satellite---Hyperion---from the very moment
of its discovery is an interesting object for celestial mechanics
due to the peculiarities of the satellite's motion caused by the attraction of
Titan---the nearest to the Hyperion and the most massive satellite
of Saturn [9,11].
The aim of this paper is to obtain a numerical theory of motion of
Hyperion that gives an accuracy comparable to the accuracy of
groundbased observations. The theory takes into account
perturbations from the Sun, Jupiter, zonal harmonics of Saturn
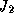 ,
, 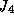 , and from the other satellites (from Mimas to
Phoebe). To avoid the accuracy loss the equations of motion were
modified using the Encke method in the form proposed by D. K.
Kulikov [7] and P. Herget [4] (see also [3]),
which gave an opportunity to obtain the right-hand parts of the
motion equations by the same technique for any perturbed body (the
Sun, Jupiter and satellites). As a reference orbit that from
[5,6] was used. The coordinates of the Sun, of
Saturn and of Jupiter were taken from the American ephemerides DE
200 [10].
, and from the other satellites (from Mimas to
Phoebe). To avoid the accuracy loss the equations of motion were
modified using the Encke method in the form proposed by D. K.
Kulikov [7] and P. Herget [4] (see also [3]),
which gave an opportunity to obtain the right-hand parts of the
motion equations by the same technique for any perturbed body (the
Sun, Jupiter and satellites). As a reference orbit that from
[5,6] was used. The coordinates of the Sun, of
Saturn and of Jupiter were taken from the American ephemerides DE
200 [10].
The modified equations of the motion of Titan and of Hyperion were
integrated by the method of rational function extrapolation [2].
The method was installed by a program at an IBM-compatible personal
computer. The program gives the accuracy not less than
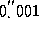 in the geocentric position of the satellite
within the time interval of 10 years.
in the geocentric position of the satellite
within the time interval of 10 years.
To improve the orbital elements I used the formulae by Yu. V.
Batrakov and T. K. Nikolskaya [1] for the unperturbed motion.
The elements to be improved are
the following six non-singular ones:
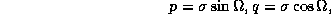
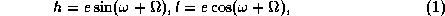

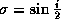 , n is the mean motion, e is the
eccentricity, i is the inclination,
, n is the mean motion, e is the
eccentricity, i is the inclination, 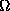 is the node
longitude,
is the node
longitude,  is the perisaturnium argument and
is the perisaturnium argument and 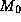 is the
mean anomaly at the moment when
is the
mean anomaly at the moment when 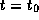 .
.




Next: Representation of the
Up:
A Theory of
Previous:
A Theory of
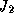 ,
, 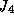 , and from the other satellites (from Mimas to
Phoebe). To avoid the accuracy loss the equations of motion were
modified using the Encke method in the form proposed by D. K.
Kulikov [7] and P. Herget [4] (see also [3]),
which gave an opportunity to obtain the right-hand parts of the
motion equations by the same technique for any perturbed body (the
Sun, Jupiter and satellites). As a reference orbit that from
[5,6] was used. The coordinates of the Sun, of
Saturn and of Jupiter were taken from the American ephemerides DE
200 [10].
, and from the other satellites (from Mimas to
Phoebe). To avoid the accuracy loss the equations of motion were
modified using the Encke method in the form proposed by D. K.
Kulikov [7] and P. Herget [4] (see also [3]),
which gave an opportunity to obtain the right-hand parts of the
motion equations by the same technique for any perturbed body (the
Sun, Jupiter and satellites). As a reference orbit that from
[5,6] was used. The coordinates of the Sun, of
Saturn and of Jupiter were taken from the American ephemerides DE
200 [10].

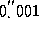 in the geocentric position of the satellite
within the time interval of 10 years.
in the geocentric position of the satellite
within the time interval of 10 years.
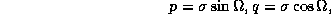
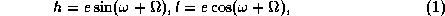

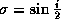 , n is the mean motion, e is the
eccentricity, i is the inclination,
, n is the mean motion, e is the
eccentricity, i is the inclination, 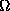 is the node
longitude,
is the node
longitude,  is the perisaturnium argument and
is the perisaturnium argument and 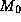 is the
mean anomaly at the moment when
is the
mean anomaly at the moment when 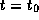 .
.