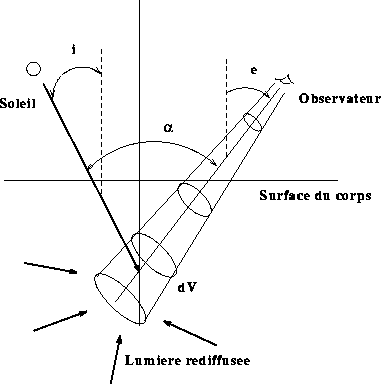
Figure: Diffusion de la lumière solaire par une surface

La figure 1 montre les principaux effets sur la forme de la courbe de lumière des paramètres de diffusion. Outre le fait que les propriétés photométriques des surfaces occultées et le paramètre d´impact du phénomène (distance minimale entre les centres de gravité des deux satellites) sont fortement corrélés dans la profondeur de la chute en magnitude observée, il existe aussi un "effet de forme" induit par certains paramètres. C´est ainsi que la pente de la chute en magnitude dépend fortement de la valeur du paramètre de rugosité macroscopique. Ceci vient du fait que près du terminateur et près du limbe, les ombres projetées deviennent importantes.

Figure: Diffusion de la lumière solaire par une surface
D´autre part, compte-tenu de l´existence d´une phase, le lieu du photocentre et le centre de gravité ne sont pas confondus. Or, la donnée accessible à une mesure directe est l´instant du minimum de lumière.
Il est cependant possible d´obtenir une expression analytique approchée de la différence entre le temps du minimum de distance et l´instant du minimum de lumière. Ce décalage est donné par:

où  est la phase, R est le rayon du satellite occulté ou
éclipsé, V est la vitesse relative entre les deux satellites et k
est le coefficient d´assombrissement de limbe de Minnaert. Cette relation
est en fait une généralisation de la relation d´[Aks86] obtenue en
supposant que l´on est en présence de diffuseurs de Lambert, ce qui correspond
en fait à un coefficient de Minnaert égal à 1.
est la phase, R est le rayon du satellite occulté ou
éclipsé, V est la vitesse relative entre les deux satellites et k
est le coefficient d´assombrissement de limbe de Minnaert. Cette relation
est en fait une généralisation de la relation d´[Aks86] obtenue en
supposant que l´on est en présence de diffuseurs de Lambert, ce qui correspond
en fait à un coefficient de Minnaert égal à 1.
On constate que le décalage photocentre-centre de gravité dépend très
peu du type de diffusion existant à la surface des corps considérés.
En effet, selon que l´on considère un corps brillant à fort assombrissement
de limbe (k=1) ou un corps sombre sans assombrissement de limbe (k=0.5), on
obtient une valeur sensiblement proche du coefficient 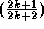 qui
est de l´ordre de 1/3.
qui
est de l´ordre de 1/3.
Cependant, dans le cas de phénomènes annulaires, cette relation ne convient plus. De plus la forme de la courbe de lumière dépend alors fortement du type de diffusion ainsi que le montre la figure 2.
Sur cette figure sont présentées la courbe de lumière observée d´une occultation annulaire
de Callisto par Europe survenue le 29 mai 1985 ainsi que trois courbes de lumière
théoriques calculées à partir de prédictions astrométriques issues
de l´éphéméride G5 et d´une modélisation de la diffusion de la
lumière à l´aide de la loi de Minnaert. Alors que la relation précédente
donne pour ce phénomène un décalage de 9.5s entre les instants de minimum
de lumière et de minimum de distance (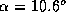 ,
, 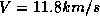 ), le
modèle indique en réalité un écart de 52.1s.
), le
modèle indique en réalité un écart de 52.1s.
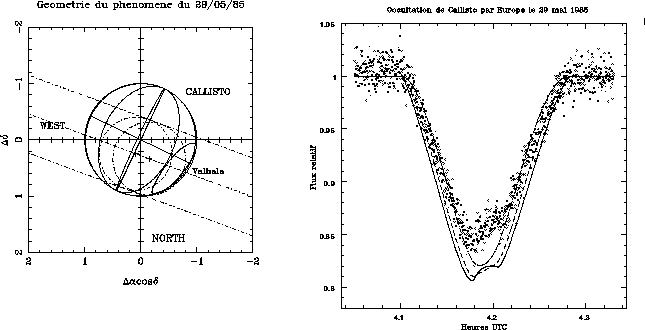
Figure: Trois courbes de prédiction, non ajustées à l´observation, sont
superposées à la courbe de lumière observée. Elles ont été obtenues
pour trois valeurs du paramètre de Minnaert: k=0.3 (traits pleins), k=0.5
(traits
interrompus) et k=1.0 (trait-point). La figure de gauche représente la
configuration géométrique du phénomène. Le mouvement du satellite
occultant se fait de l´est vers l´ouest. Le disque d´Europe (en pointillés) est
tracé aux instants du minimum de lumière et du minimum de distance.
Il apparait alors nettement que la loi de Lambert (k=1) ne peut rendre compte du comportement diffusant de la surface de Callisto qui est du reste un corps sombre.
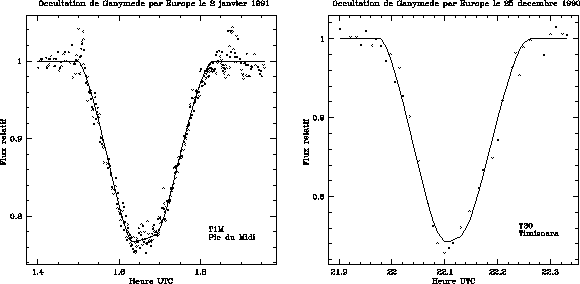
Figure: Courbes de lumière de deux phénomènes annulaires
En fait, si l´on réalise l´ajustement de cette observation, on obtient une valeur du coefficient de Minnaert égale à 0.46. C´est-à-dire que l´on est en présence d´une légère brillance de limbe. Ceci peut s´expliquer si l´on se reporte à la configuration géométrique du phénomène qui montre Callisto présentant sur son limbe un grand bassin brillant connu sous le nom de Valhala et qui contribue donc à créer cette légère brillance de limbe.
Sur la figure 3 sont présentées deux courbes de lumière de phénomènes annulaires observés en 1991. Chacune de ces observations a été ajustée à l´aide du modèle précédemment évoqué.
