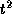 sur une longue
série d´observations.
Le décalage en longitude de la
position du satellite du fait de cette accélération est donné par
sur une longue
série d´observations.
Le décalage en longitude de la
position du satellite du fait de cette accélération est donné par

La détermination d´une accélération séculaire dans le moyen mouvement
d´un satellite naturel se fait par l´ajustement, dans le
modèle dynamique du mouvement de ce corps, d´un terme en 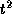 sur une longue
série d´observations.
Le décalage en longitude de la
position du satellite du fait de cette accélération est donné par
sur une longue
série d´observations.
Le décalage en longitude de la
position du satellite du fait de cette accélération est donné par

Cette expression donne la longitude relativement à celle que l´on aurait si le mouvement n´était pas accéléré, comptée à partir d´un instant arbitraire t=0.
Jusqu´à présent, outre la Lune, la mesure d´une éventuelle accélération séculaire n´a été faite que pour deux corps pour lesquels on dispose d´observations sur une durée assez longue, Io et Mimas. La table 1 donne les mesures des accélérations séculaires de chacun de ces deux satellites ainsi que les écarts en longitude engendrés dans leur position orbitale pour une durée égale à la durée des observations disponibles.

Table:
Mesures des accélérations séculaires de Io et Mimas
La mesure la plus récente de l´accélération de Io est celle de [Lie87], faite à partir d´une collection d´observations d´éclipses par la planète allant de 1652 à 1983 et également d´observations photographiques faites par Pascu entre 1967 et 1978. Quelques observations de phénomènes mutuels de 1973 et 1979 réduites par Aksnes et al.(1984) furent également utilisées.
Bien qu´il soit possible de rapporter chacune de ces observations en temps universel (UT), même pour les plus anciennes d´entre elles, pourtant éffectuées en temps local apparent, il est par contre plus difficile de les exprimer en temps des éphémérides (ET), échelle de temps uniforme utilisée dans les éphémérides.
Généralement la détermination de 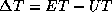 se fait à
partir d´observations de la Lune du fait du mouvement rapide de celle-ci.
Des tables donnant le
se fait à
partir d´observations de la Lune du fait du mouvement rapide de celle-ci.
Des tables donnant le 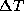 ont été publiées mais une
complication supplémentaire surgit du fait que la Lune a elle aussi sa
propre accélération qui affecte donc sa longitude. Les tables donnant
le
ont été publiées mais une
complication supplémentaire surgit du fait que la Lune a elle aussi sa
propre accélération qui affecte donc sa longitude. Les tables donnant
le 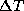 à toute époque doivent donc adopter ou estimer une
valeur de cette accélération. En conséquence, la détermination d´une
accélération séculaire basée sur des observations anciennes dépend
, de manière critique, de la valeur de ce paramètre. A la relative imprécision
des observations anciennes s´ajoute donc ce problème supplémentaire qui
rend donc la mesure extrêmement délicate voire douteuse.
à toute époque doivent donc adopter ou estimer une
valeur de cette accélération. En conséquence, la détermination d´une
accélération séculaire basée sur des observations anciennes dépend
, de manière critique, de la valeur de ce paramètre. A la relative imprécision
des observations anciennes s´ajoute donc ce problème supplémentaire qui
rend donc la mesure extrêmement délicate voire douteuse.
La valeur obtenue par Lieske est très faible et suggère un ralentissement de Io sur son orbite, c´est-à-dire un éloignement par rapport à Jupiter. Les effets de marée engendrées par Io sur Jupiter semblent donc dominer l´évolution orbitale.
En ce qui concerne la supposée accélération de Mimas, elle fut détectée pour la première fois par [Koz57] et confirmée par [Dou87] qui comparèrent leurs théories aux 100 années d´observations disponibles. Mais [DV91] montrèrent à travers leur nouvelle théorie que cette accélération provenait tout simplement de l´absence de certains termes à longue période dans les précédents modèles dynamiques. L´ajustement d´une parabole sur les séries de termes à longue période nouvellement introduits et représentant la longitude moyenne permis de retrouver la valeur de l´accélération de Kozai et Dourneau. De plus [Sar92] vint confirmer ce résultat en donnant une borne supérieure à l´accélération de Mimas en se basant sur le taux de dissipation minimum possible dans l´intérieur de Saturne
Finalement, si l´on admet que l´ordre de grandeur des accélérations séculaires
à mesurer est de 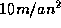 et que l´on désire effectuer cette détermination à
partir des observations les plus récentes et les plus précises (observations
photographiques depuis 1890 et phénomènes mutuels) collectées depuis près de
100 ans, il faut être en mesure de pouvoir détecter un décalage en longitude
de l´ordre de 50km (
et que l´on désire effectuer cette détermination à
partir des observations les plus récentes et les plus précises (observations
photographiques depuis 1890 et phénomènes mutuels) collectées depuis près de
100 ans, il faut être en mesure de pouvoir détecter un décalage en longitude
de l´ordre de 50km (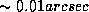 ) dans le cas des satellites de Saturne ! Ce qui nécessite des observations dont la précision
est de cet ordre.
) dans le cas des satellites de Saturne ! Ce qui nécessite des observations dont la précision
est de cet ordre.
Aux difficultés inhérentes à la détermination de l´accélération séculaire vient s´ajouter un effet linéaire relativiste à long terme provenant de l´avance du péricentre. Cette avance du péricentre sur une période orbitale est donnée par la formule approchée classique:

où a est le demi-grand axe de l´orbite du satellite et m le rayon
relativiste de la planète mère donné par 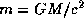 . Ainsi,
pour Jupiter dont le rayon relativiste est de 1.4m on a une avance du
périjove de Io de 5.2km/an et pour Saturne dont le rayon relativiste est de
0.42m, l´avance du pericentre de Mimas atteint 3.1km/an. Si l´on compare l´effet de
cette avance sur des intervalles
de temps semblables aux durées pour lesquelles on dispose d´observations,
à l´effet engendré par l´existence d´une accélération du moyen mouvement
, on constate qu´ils peuvent être du même ordre de grandeur.
. Ainsi,
pour Jupiter dont le rayon relativiste est de 1.4m on a une avance du
périjove de Io de 5.2km/an et pour Saturne dont le rayon relativiste est de
0.42m, l´avance du pericentre de Mimas atteint 3.1km/an. Si l´on compare l´effet de
cette avance sur des intervalles
de temps semblables aux durées pour lesquelles on dispose d´observations,
à l´effet engendré par l´existence d´une accélération du moyen mouvement
, on constate qu´ils peuvent être du même ordre de grandeur.
Or les modèles dynamiques actuels ne prennent pas encore en compte les corrections relativistes considérées comme négligeables devant la précision des observations.
La détermination d´une accélération séculaire dans le mouvement d´un satellite est donc extrêmement difficile. Elle nécessite d´une part des modèles dynamiques très évolués prenant en compte tous les termes à longue période mais également les effets relativistes à long terme et d´autre part des observations très précises réparties sur une base de temps assez longue.
